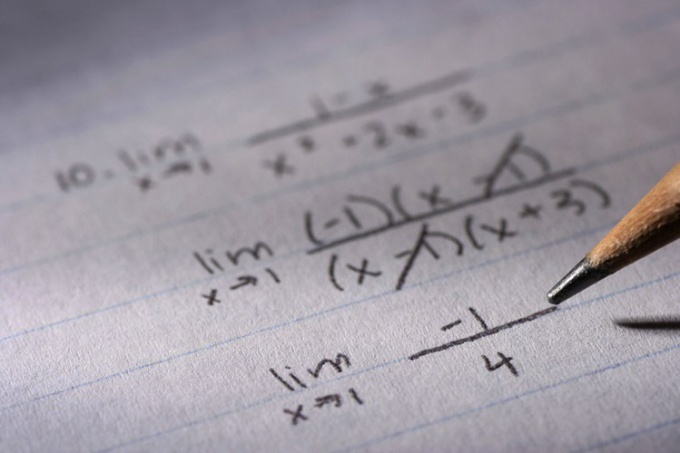Tip 1: How to simplify expression
Tip 1: How to simplify expression
To quickly and efficiently perform calculations, simplify mathematical expressions. To do this, use mathematical relationships to make the expression shorter, and simplify calculations.
You will need
- - the concept of a monomial of a polynomial;
- - reduced multiplication formulas;
- - actions with fractions;
- basic trigonometric identities.
Instructions
1
If the expression contains monomials with identical factors, find the sum of the coefficients for them and multiply them by a multiplier. For example, if there is an expression 2 • a-4 • a + 5 • a + a = (2-4 + 5 + 1) ∙ a = 4 ∙ a.
2
To simplify the expression, use formulasreduced multiplication. The most popular are the square of the difference, the difference of squares, the difference and the sum of the cubes. For example, if there is an expression of 256-384 + 144, imagine it as 16²-2 • 16 • 12 + 12² = (16-12) ² = 4² = 16.
3
In the event that the expression isa natural fraction, select a common factor from the numerator and denominator and reduce the fraction to it. For example, if you want to reduce the fraction (3 • a²-6 • a • b + 3 • b²) / (6 ∙ a²-6 ∙ b²), remove the common factors in the numerator from the numerator and the denominator, this will be 3, in the denominator 6. Get expression (3 • (a²-2 • a • b + b²)) / (6 ∙ (a²-b²)). Reduce the numerator and denominator by 3 and apply the reduced multiplication formula to the remaining expressions. For the numerator this is the square of the difference, and for the denominator the difference of the squares. Obtain the expression (ab) ² / (2 ∙ (a + b) ∙ (ab)) by reducing it to a common factor ab, get the expression (ab) / (2 ∙ (a + b)), which is much easier for specific values of variables to count.
4
If the monomials have the same factors,raised to a power, then when summing them, make sure that the degrees are equal, otherwise you can not reduce these. For example, if there is an expression of 2 ∙ m² + 6 • m³-m²-4 • m³ + 7, then if you reduce these, you will get m² + 2 • m³ + 7.
5
If we simplify trigonometric identitiesuse formulas to convert them. The basic trigonometric identity is sin2 (x) + cos2 (x) = 1, sin (x) / cos (x) = tg (x), 1 / tg (x) = ctg (x), the sum and difference formulas of arguments double, triple argument and others. For example, (sin (2 ∙ x) - cos (x)) / ctg (x). Describe the formula of the double argument and cotangent, as the ratio of the cosine to the sine. Obtain (2 ∙ sin (x) • cos (x) - cos (x)) • sin (x) / cos (x). Take the common factor, cos (x) and shorten the fraction cos (x) • (2 ∙ sin (x) - 1) • sin (x) / cos (x) = (2 ∙ sin (x) - 1) • sin ( x).
Tip 2: How to Simplify Expressions
Brevity, as they say, is the sister of talent. Everyone wants to show off a talent, but his sister is a complicated thing. Brilliant thoughts for some reason themselves are put on in complex sentences with a lot of participial turns. However, in your power to simplify your proposals and make them understandable and accessible to all.
Instructions
1
To facilitate the addressee (be it a listener orreader) life, try to replace participial and adverbial movements with short subordinate clauses, especially if the above mentioned turns are too much in one sentence. "A cat coming home, a mouse that had just eaten, loudly purring, caressed the owner, trying to look into his eyes, hoping to get the fish brought from the store" - this will not work. Break up such a construction into several parts, take your time and do not try to say everything with one sentence, and you will be happy.
2
If you conceived a brilliant statement, but inIt turned out to be too many subordinate clauses (especially with one union), it is better to split the statement into several separate sentences or omit some element. "We decided that he would tell Marina Vasilyevna that Katya would tell Vita that ..." - it is possible to continue indefinitely. Stop in time and remember the person who will read it or listen.
3
However, the pitfalls lie not only in thestructure of the proposal. Pay attention to the vocabulary. Foreign words, long terms, words drawn from fiction of the 19th century - all this will only complicate the perception. It is necessary to clarify for yourself, for which audience you are composing the text: technicians, of course, will understand both complex terms and specific words; But if you offer the same words to a teacher of literature, she is unlikely to understand you.
4
Talent is a great thing. If you are talented (and there are no people without abilities), many roads open before you. But the talent is not in complexity, but simplicity, oddly enough. Be simpler, and your talents will be understandable and accessible to all.
Tip 3: How to simplify the fractional expression
«Expression"In mathematics is usually called the setArithmetic and algebraic actions with numbers and variable values. By analogy with the format of writing numbers, such a set is called "fractional" when it contains a division operation. To the fractional expressions, as to numbers in the ordinary fraction format, simplification operations are applicable.
Instructions
1
Start by finding the common factor forexpressions that stand in the numerator and denominator of the fraction - this rule is the same for both numerical relationships and for variables that contain unknowns. For example, if the numerator is 45 * X, and the denominator is 18 * Y, then the greatest common multiplier is 9. After this step, the numerator can be written as 9 * 5 * X, and the denominator as 9 * 2 * Y.
2
If the expressions in the numerator and denominator containa combination of basic mathematical operations (multiplication, division, addition and subtraction), you first have to take the common factor for each of them separately, and then extract the greatest common divisor from these numbers. For example, for the expression 45 * X + 180 standing in the numerator, the multiplier 45: 45 * X + 180 = 45 * (X + 4) should be taken outside the brackets. And the expression 18 + 54 * Y in the denominator must be reduced to the form 18 * (1 + 3 * Y). Then, as in the previous step, find the greatest common divisor of the multipliers: * * (X + 4) / 9 * 2 * (1 + 3 * Y). In this example, it is also equal to nine.
3
Cut the total in the previous stepsmultiplier of expressions in the numerator and denominator of the fraction. For an example from the first step, the entire simplification operation can be written as: 45 * X / 18 * Y = 9 * 5 * X / 9 * 2 * Y = 5 * X / 2 * Y.
4
Not necessarily with the simplification of the generaldivisor must be a number, it can be an expression containing a variable. For example, if (4 * X + X * Y + 12 + 3 * Y) is in the numerator of the fraction, and in the denominator (X * Y + 3 * Y - 7 * X - 21), the greatest common divisor is the expression X + 3, which should be shortened to simplify the expression: (4 * X + X * Y + 12 + 3 * Y) / (X * Y + 3 * Y - 7 * X-21) = (X + 3) * (4 + Y) / (X + 3) * (Y-7) = (4 + Y) / (Y-7).
