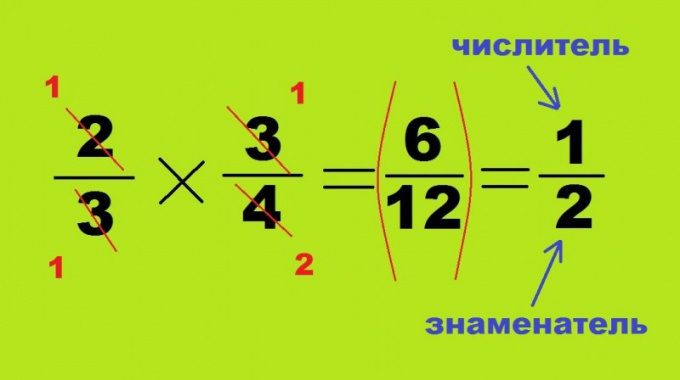To simplify the fractional rational expression,it is necessary to perform arithmetic operations in a certain order. First, the actions are performed in parentheses, then multiplication and division, and, lastly, addition and subtraction. The numerator and denominator of the original fractions are usually decomposed into multiples, because in the course of solving the example, they can be reduced.
Instructions
1
Examples</a>/ strong "class =" colorbox imagefield imagefield-imagelink "rel =" gallery-step-images "> When adding or subtracting fractions, bring them tocommon denominator. To do this, first find the least common multiple of the denominator coefficients. In this example, it is 12. Calculate the expression for the common denominator. Here: 12xy². Divide the common denominator by each of the fractional denominators. 12xy²: 4y² = 3x and 12xy²: 3xy = 4y.
2
The resulting expressions are additionalmultipliers for the first and second fractions, respectively. Multiply the numerator and denominator of each fraction by the desired additional factor. Convert the amount into a fraction. In this example, get: (3x² + 20y) / 4xy³.
3
To add a fractional expression and an integer, represent the integer as a fraction. The denominator can be any. For example, 4 = 4 ∙ a² / a²; y = y ∙ 5b / 5b, and so on.
4
To add fractions with a polynomial in the denominator,First, factor the factor. So, for this example, the denominator of the first fraction is ax-x² = x (a-x). Move in the denominator of the second fraction: x-a = - (a-x). Give the fraction to the common denominator x (a-x). In the numerator you get the expression a²-x². Divide it by the factors a²-x² = (a-x) (a + x). Fraction reduce by a-x. Get in the answer: a + x.
5
To multiply one fraction by another, multiplyamong themselves numerators and denominators of fractions. So, in this example, get the numerator y² (x²-xy) and the denominator yx. Put the total multiplier in the numerator for the brackets: y² (x²-xy) = y²x (x-y). Cut the fraction by yx, you end up with y (x-y).
6
To divide one fractional expression into another,multiply the numerator of the first fraction by the denominator of the second. In the example: 6 (m + 3) ² (m²-4). Write this expression in the numerator. Multiply the denominator of the first fraction by the numerator of the second: (2m-4) (3m + 9). Write down this expression in the denominator. Divide the polynomials into multipliers: 6 (m + 3) ² (m²-4) = 6 (m + 3) (m + 3) (m-2) (m + 2) and (2m-4) (3m + 9 ) = 2 (m-2) 3 (m + 3) = 6 (m-2) (m + 3). Cut the fraction by 6 (m-2) (m + 3). Get: (m + 3) (m + 2) = m² + 3m + 2m + 6 = m² + 5m + 6.