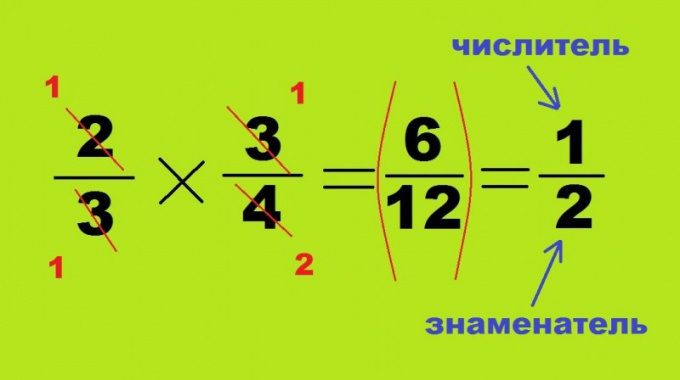Tip 1: How to compare fractions without leading to a common denominator
Tip 1: How to compare fractions without leading to a common denominator
To compare fractions with different denominators andnumerators, you need to convert them. To do this, in most cases, fractions lead to a common denominator, but there are other ways to do this.
You will need
- - a pen;
- - notebook;
- - a pencil;
- - compasses.
Instructions
1
One of the methods of comparing ordinary fractions withdifferent numerators and denominators (without bringing them to a common denominator) - a comparison with a half. For example, you need to know that more than 5/9 or 3/7. Compare these two fractions with half, that is 1/2.
2
For greater clarity, draw a circle in which sign 3/8, 1/2 and 5/9. Then compare 3/8 and 1/2 (3/8 less than 1/2). Comparing 5/9 with 1/2, you will find that 5/9 is more than 1/2.
3
With the help of this technique, it is easy to prove that 5/9 is more than 3/8. This method is convenient, since it helps visually to present the compared values.
4
The second way of comparing ordinary fractions withouttheir reduction to the common denominator - the method of addition to unity. For example, you need to determine that more than 46/47 or 47/48. It turns out that to add the first fraction to one it is necessary to increase it by 1/47, and the second - to add to it 1/48.
5
If you compare 1/48 and 1/47 (for example, with the help ofcircle), it is seen that 1/48 is less than 1/47. Thus, 47/48 is greater than 46/47: to increase 47/48 to one, a fraction is required with a smaller value than for an increase of 46/47.
6
The third method of comparing fractions is based onthe assertion that "an improper fraction is always more correct." Wrong is a fraction whose numerator is greater than or equal to the denominator. Consequently, a fraction whose numerator is less than its denominator is called correct.
7
For example, you need to compare 5/4 and 3/5. Considering the fact that 5/4 is an incorrect fraction, and 3/5 is correct, it is easy to conclude that the first is greater than the second. This is true, since 5/4 is greater than one, and 3/5 is less than one.
Tip 2: How to lead to a common denominator
Often when working with fractions, it becomes necessary to add or subtract them. To do this, you need to add fractions to the total denominator. The ordinary fraction consists of two parts: the divisible and the divisor, which are called the numerator and denominator, respectively.
You will need
- Basic knowledge in mathematics.
Instructions
1
Suppose you have two fractions: 2/3 and 7/8. First, we find the smallest common divisible denominator of these fractions, and then we give both fractions to it. In our case, the smallest common divisible is the number 24, so we will bring fractions to it.
2
To bring the first fraction to the foundthe smallest common divisible, multiply the numerator of the first fraction by the quotient of dividing this divisor by the numerator. In our case this will be: 24/3 = 8. That is, the numerator of the first fraction must be multiplied by 8. Similarly, we find the factor for the second fraction: 24/8 = 3. That is, the numerator of the second fraction must be multiplied by 3.
3
We multiply the numerators of the fractions by the partial fractions obtained. As a result, the fractions will have a common denominator: 16/24 and 21/24.
Tip 3: How to compare fractions with different denominators
To compare Fractions with the same denominators, you just need to compare their numerators. The situation is somewhat different in the case when two fractions are different in the denominator. Here you need to perform a little more action.
You will need
- paper
- pen or pencil
Instructions
1
Fractions with different numerators and denominatorscan not be compared without their transformation. A fraction can be reduced to any denominator, the multiple denominator of this fraction. This means that the new denominator must be divided entirely on the denominator of this fraction. For example, the new denominator of the 3/8 fraction may be the denominator 32, since 32 is divided by 8 in its entirety.
2
Divide the new denominator into the old one. 32: 8 = 4. You got an additional multiplier.
3
To bring the fraction to a new denominator,multiply its numerator and multiplier by an additional factor. For example, if you want to cast a 3/8 fraction to the denominator 32, multiply both 3 and 8 by 4.
4
Now give the fractions that you needcompare, to the common denominator. To compare two fractions, take the product of their denominators for the common denominator, since this number will be a multiple of both denominators. Such a number is called the smallest common denominator. Let's say you need to compare fractions 5/7 and 3/5. First multiply the denominators. When multiplying 7 by 5, we get 35. This is the common denominator.
5
An additional factor for the fraction 5/7 is the number 5, since 35: 7 = 5. Multiply the numerator and denominator of the fraction by 5. We get 25/35.
6
An additional factor for the fraction 3/5 is the number 7, since 35: 5 = 7. Multiply the numerator and the denominator of the fraction by 7. We get 21/35.
7
Now compare the resulting fractions. The larger (smaller) is the fraction whose numerator is larger (less). 25/35> 21/35. Therefore, 5/7> 3/5. The problem is solved successfully.
Tip 4: How to bring a fraction to the smallest common denominator
When performing arithmetic operations with simplefractions inevitably raises the question of how to add them or subtract them from one another if there are different numbers in the denominators? It is necessary to bring fractions to some general form, so that it is clear which parts of an integer are added or subtracted. That is, it is necessary to bring the fraction to the lowest common denominator.
You will need
- - paper;
- - pen or pencil;
- - calculator.
Instructions
1
Write an example. Let's say you need to add 2 / a and 5 / b fractions. Instead of letters there can be any numbers. Look at what stands in the numerator and denominator of each fraction and whether one of them or both can be cut. It is advisable to do this in any case, regardless of whether the same denominators result from this action or not. For example, if you need to add 1/3 and 4/6, you need to cut the second fraction. Remember the rule of contraction. The numerator and denominator must be divided into one and the same number. In the example above, they are divided by 2. It turns out that 4/6 = 2/3, that is, 1/3 it is necessary to add 2/3. The result is one.
2
If the fractions do not shrink or as a resultDifferent denominators are obtained, it is necessary to find a common denominator. Remember the property of a fraction, according to which its value does not change if the upper and lower parts are multiplied by the same number. This number is called an additional factor. Find it for fractions 2 / a and 5 / b. In this case, it is necessary to multiply the denominators, that is, the additional factor will be equal to a * b.
3
Calculate, on what number it is necessary to multiplyeach of the fractions, in order to obtain the same denominators. For the first fraction this will be the number b, for the second - the number a. Thus, each fraction can be represented in the form 2 / a = 2b / ab; 5 / b = 5a / ab. In this case, you can already find the sum or difference of fractions. The sum m = 2b / ab + 5a / ab = (2b + 5a) / ab. In exactly the same way, there is a common denominator for three or more fractions.
4
For the convenience of calculations, fractions usually lead tothe smallest common denominator. It is equal to the smallest common multiple of the numbers that stand in the denominators of all data under the conditions of the fractional problem. Remember how the least common multiple is calculated. It is the smallest number that is divisible by all the original numbers. To do this, decompose each number into prime factors. To calculate the least common multiple, multiply them. Each simple multiplier must be taken as many times as it occurs in the number where it is greatest. For example, if you need to find the smallest common multiple of numbers 10, 16 and 26, decompose them as follows. 10 = 2 * 5, 16 = 2 * 2 * 2 * 2, 26 = 2 * 13. LOC = 5 * 2 * 2 * 2 * 2 * 13 = 1040. From this example it is clear that a simple multiplier 2 must be taken as many times as the number 16 is decomposed.
