LovesTheTeam.com

Instructions

1

2

Consider the triangle ABD. The length of its side AB is equal to the modulus of the vector a. Suppose that | a | = sqrt ((ax) ^ 2 + (ay) ^ 2) = a, then cosφ = ax / sqrt (((ax) ^ 2 + (ay) ^ 2) as the directing cosine of a. diagonal BD has long p, and the desired AD long x. Then, by the cosine theorem, P ^ 2 = a ^ 2 + x ^ 2-2axcosφ. Or x2 2axcosφ + (a ^ 2-p ^ 2) = 0.

3

The solutions of this quadratic equation are: X1 = (2acosf + sqrt (4 (a ^ 2) ((cosφ) ^ 2) -4 (a ^ 2-p ^ 2))) / 2 = acosf + sqrt ((a ^ 2) ((cosφ) ^ 2) - (a ^ 2-p ^ 2)) = a * ax | sqrt (((ax) ^ 2 + (ay) ^ 2) + sqrt ((((a) ^ 2) (ax ^ 2)) / (ax ^ 2 + ay ^ 2)) - a ^ 2 + p ^ 2) = AD.

4

To find the upper foundations BC (its length in the search for a solution is also denoted by x), the module | a | = a is used, and also the second diagonal BD = q and the cosine of the angle ABC, which is obviously equal to (n-φ).

5

The triangle ABC, kwhich, as before, the cosine theorem is applied, and the following solution arises. Taking into account that cos (n-φ) = -cosφ, on the basis of the solution for AD, we can write the following formula, replacing p by q: BC = - a * ax | sqrt (((ax) ^ 2 + (ay) ^ 2 ) + sqrt ((((a) ^ 2) (ax ^ 2)) / (ax ^ 2 + ay ^ 2)) - a ^ 2 + q ^ 2).

6

This equation is square and,accordingly, has two roots. Thus, in this case it remains only to choose those roots that have a positive value, since the length can not be negative.

7

Example Trapezoid The ABCD side of AB is given by the vector a (1, sqrt3), p = 4, q = 6. To find foundations Trapezoid.Decision. Using the algorithms obtained above, we can write: | a | = a = 2, cosφ = 1/2. AD = 1/2 + sqrt (4/4 -4 + 16) = 1/2 + sqrt (13) = (sqrt (13) +1) /2.BC=-1/2+sqrt (-3 + 36 ) = (sqrt (33) -1) / 2.

You will need

• Knowledge of the sides, bases, middle line of the trapezoid, as well as, optionally, its area and / or perimeter.

Instructions

1

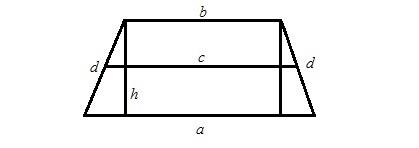
One way to calculate the area of ​​the trapezoidis the product of height and center line. Assume that there is an isosceles trapezoid. Then the height of an isosceles trapezium with bases a and b, area S and perimeter P will be calculated as follows: h = 2 x S / (P-2 x d). (see Figure 1)

2

If only the area of ​​the trapezium and its base are known, then the height calculation formula can be derived from the trapezium area formula S = 1 / 2h x (a + b): h = 2S / (a ​​+ b).

3

Suppose there is a trapezoid with the same data asand in Figure 1. We draw 2 heights, we obtain a rectangle, in which the two smaller sides are the legs of right-angled triangles. Let us denote the smaller one for x. It is found by dividing the difference in length between the larger and smaller bases. Then, by the Pythagorean theorem, the square of the height is equal to the sum of the squares of the hypotenuse d and the x-ray. We extract the root from this sum and get the height h. (Figure 2)

Instructions

1

Task 1. Find the bases of BC and AD rectangular Trapezoidif the length of the diagonal AC = f is known; lengthlateral side CD = c and the angle with it ADC = α. Solution: Consider the rectangular triangle CED. Known hypotenuse c and the angle between the hypotenuse and the leg of the EDC. Find the lengths of the sides CE and ED: according to the angle formula CE = CD * sin (ADC); ED = CD * cos (ADC). So: CE = c * sinα; ED = c * cosα.

2

Consider the right triangle ACE. Hypotenuse AC and CE are known to you, find side AE ​​according to the rule of a right triangle: the sum of the squares of the legs is equal to the square of the hypotenuse. So: AE (2) = AC (2) - CE (2) = f (2) - c * sinα. Calculate the square root of the right side of the equation. You found the top base of a rectangular Trapezoid.

3

The length of the base AD is the sum of the lengths of twosegments AE and ED. AE = square root (f (2) - c * sinα); ED = c * cosα). So: AD = square root (f (2) - c * sinα) + c * cosα. You found the bottom base of a rectangular Trapezoid.

4

Task 2. Find the bases of BC and AD rectangular Trapezoidif the length of the diagonal BD = f is known; lengthlateral side CD = c and the angle with it ADC = α. Solution: Consider the rectangular triangle CED. Find the lengths of the CE and ED sides: CE = CD * sin (ADC) = c * sinα; ED = CD * cos (ADC) = c * cosα.

5

Consider the ABCE rectangle. By the property of the rectangle AB = CE = c * sinα. Consider the right triangle ABD. By the property of a right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs. Therefore, AD (2) = BD (2) - AB (2) = f (2) - c * sinα. You found the bottom base of a rectangular Trapezoid AD = square root (f (2) - c * sinα).

6

By the rule of the rectangle BC = AE = AD - ED = square root (f (2) - c * sinα) - c * cosα. You found the upper base of a rectangular Trapezoid.

You will need

• - calculator.

Instructions

1

If two lengths are known - a large basetrapezium and midline - use the trapezium property to calculate the smallest base. According to him, the middle line of the trapezoid is identical to the half-sum of the bases. In this case, the smallest base will be equal to the difference of the doubled length of the midline and the length of the large base of this figure.

2

If you know such trapezoid parameters asarea, height, length of a large base, then calculate the smallest base of this figure based on the trapezoid area formula. In this case, the final result is obtained by subtracting from the difference of the quoted double area and the height of such a parameter as the length of the large base of the trapezoid.

3

The length of the smallest side in a rectangularTrapezium calculate by another method. This parameter will be equal to the product of the length of the second side and the sine of the acute angle adjacent to it. In the same cases, when the value of the angle is unknown, equate the smallest side side to the height of the trapezoid and calculate it according to the Pythagorean theorem. The smallest side in the rectangular trapezoid is found using the cosine theorem: c² = a² + b²-2ab * cosα; where a, b, c represent the sides of the triangle; α is the angle between sides a and b.

Instructions

1

Of the three heights of the triangle,which is lowered to the largest of the sides of the figure. To see this, express all three heights of the triangle through the dimensions of its sides and compare. Suppose that the side a is the largest of the three sides a, b, c of an arbitrary acute-angled triangle, the side c is the smallest. We denote the height h on the side a, hb the height drawn to the side b, hc the height to the side c. Height divides any triangle into two rectangular triangles, in which this height will always be one of the legs.

2

The height ha, drawn to the largest side of a,can be determined by the Pythagoras theorem: hа² = b² - а₁² or hа² = с² - а₂². Where a₁ and a₂ are the segments to which the side a is divided by the height ha. Also, by the Pythagorean theorem, express the other two heights of the triangle through its sides: hb ² = a²-b₁² or hb² = c²-b₂²; hc² = a²-c₁² or hc² = b²-c₂².

3

From a comparison of the formulas determining the heightstriangle, it is obvious that the ratio between the decreased and the subtracted yields the smallest difference in the expressions hа² = b² - а₁² and hа² = с²-а₂², because the subtrahend a₁ and а₂ are the segments of the largest side of the triangle.

4

To determine the smaller height of the triangle, you canalso through the sine of the known angle of the triangle. If by the condition the greatest of the angles is given, then this angle lies against the greatest side, and from it the least height is drawn. To avoid cumbersome calculations, it is better to express the desired height through the trigonometric functions of the other two angles of the triangle, since the ratio of the side of the triangle to the sine of the opposing angle is a constant for a given triangle. Consequently, the smallest height of the triangle ha = b * SinB or ha = c * SinC, where B is the angle between the largest side of a and side b, and C is the angle between the largest side of a and the side of the triangle.