Tip 1: How to derive the triangle median formula

The science

Tip 1: How to derive the triangle median formula

The median in the triangle is the segment that is drawn from the top of the corner to the middle of the opposite side. To find the length Medians, it is necessary to use the formula for expressing it through all sides triangle, which is not difficult to deduce.

Instructions

To deduce Formula for Medians in an arbitrary triangle, it is necessary to turn to the corollary of the cosine theorem for a parallelogram obtained by completing triangle. The formula can be proved on this basis, it is very convenient for solving problems if all the lengths of the sides are known or can easily be found from other initial data of the problem.

In fact, the cosine theorem is a generalization of the Pythagorean theorem. It sounds like this: for two-dimensional triangle With the lengths of sides a, b and c and angle α, opposite side a, the following equality holds: a² = b² + c² - 2 • b • c • cos α.

The generalizing corollary of the cosine theorem determines one of the most important properties of a quadrangle: the sum of the squares of the diagonals is equal to the sum of the squares of all its sides: d1² + d2² = a² + b² + c² + d².

Solve the problem: let all sides be known in an arbitrary triangle ABC, find its median BM.

Complete the triangle to the parallelogram ABCDAdding lines parallel to a and c. Thus, a figure with sides a and c and diagonal b was formed. The most convenient way to build this is as follows: put the MD segment of the same length on the continuation of the straight line to which the median belongs, connect its vertex to the vertices of the remaining two sides A and C.

By the property of a parallelogram, the diagonals dividepoint of intersection into equal parts. Apply the corollary of the cosine theorem, according to which the sum of the squares of the parallelogram diagonals is equal to the sum of the doubled squares of its sides: BK² + AC² = 2 • AB² + 2 • BC².

Since BK = 2 • BM and BM is the median m, then: (2 • m) ² + b² = 2 • c² + 2 • a², whence: m = 1/2 • √ (2 • c² + 2 • a² - b²).

You withdrew Formula one of the medians triangle for the side b: mb = m. Similarly there are Medians Its other two sides: ma = 1/2 • √ (2 • c² + 2 • b²-a²); mc = 1/2 • √ (2 • a² + 2 • b²-c²).

Tip 2: How to find the median of a triangle

Median triangle A segment connecting any vertex triangle with the middle of the opposite side. Three medians intersect at one point always inside triangle. This point divides each median in the ratio of 2: 1.

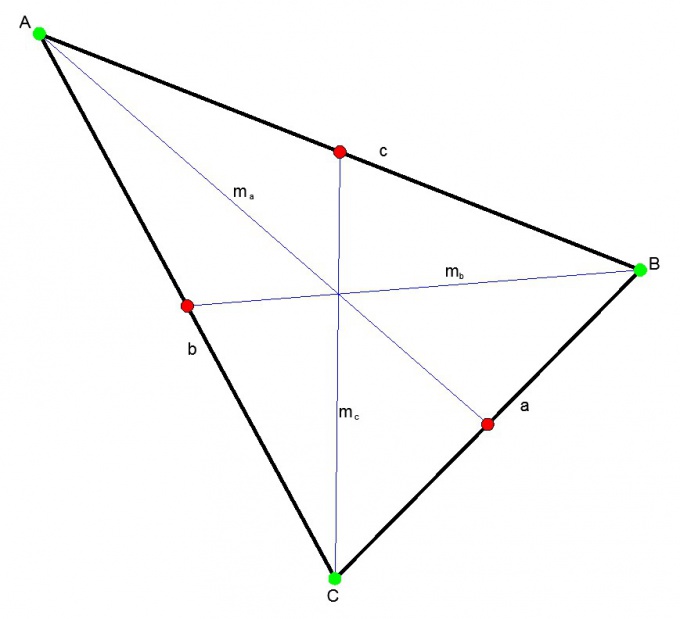
Instructions

The median can be found using Stewart's theorem. According to this, the square of the median is equal to a quarter of the sum of the doubled sides squares minus the square of the side to which the median is drawn. Mc ^ 2 = (2a ^ 2 + 2b ^ 2 - c ^ 2) / 4, where a, b, c are sides triangle.mc is the median to side with;

The problem of finding a median can be solved through additional constructions triangle up to a parallelogram and a solution via the parallelogram theorem on diagonals. triangle and median, completing them to a parallelogram. Thus, the median triangle will be equal to half the diagonal of the resulting parallelogram, the two sides triangle - its sides (a, b), and the third party triangle, To which the median was performed, isthe second diagonal of the resulting parallelogram. According to the theorem, the sum of the squares of the diagonals of the parallelogram is equal to twice the sum of the squares of its sides.2 * (a ^ 2 + b ^ 2) = d1 ^ 2 + d2 ^ 2, where d1, d2 are the diagonals of the resulting parallelogram, hence: d1 = 0.5 * v 2 * (a ^ 2 + b ^ 2) - d2 ^ 2)

Tip 3: How to find the median of a triangle on its sides

The median is the segment connecting the vertex triangle And the middle of the opposite side. Knowing the lengths of all three sides triangle, you can find his medians. In particular cases of isosceles and equilateral triangle, Obviously, enough knowledge, respectively, two (not equal to each other) and one side triangle.

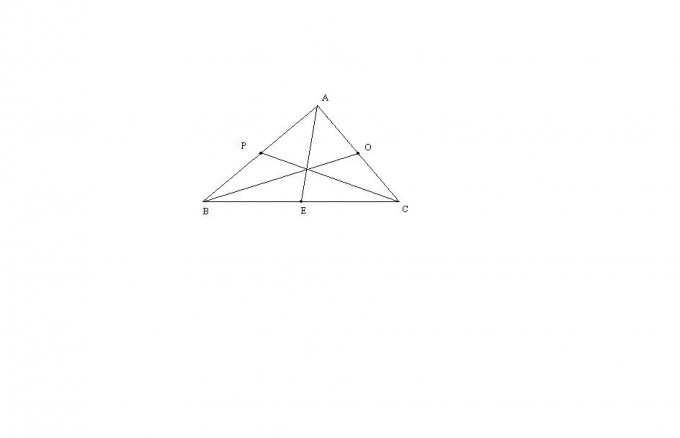
You will need

Ruler

Instructions

Let us consider the most general case triangle ABC with three not equal to each other The parties. The length of the median AE of this triangle Can be calculated by the formula: AE = sqrt (2 * (AB ^ 2) + 2 * (AC ^ 2) - (BC ^ 2)) / 2. The remaining medians are completely analogous. This formula is derived via Stewart's theorem, or through completion triangle before parallelogram.

If the triangle ABC is isosceles and AB = AC, then the median AE will be both the height of this triangle. Consequently, the triangle BEA will be rectangular. By the Pythagorean theorem, AE = sqrt ((AB ^ 2) - (BC ^ 2) / 4). From the general formula for the length of the median triangle, For medians BO and CP it is valid: BO = CP = sqrt (2 * (BC ^ 2) + (AB ^ 2)) / 2.

If the triangle ABC is equilateral, then obviously all its medians are equal to each other. Since the angle at the vertex of an equilateral triangle Is equal to 60 degrees, then AE = BO = CP = a * sqrt (3) / 2, where a = AB = AC = BC - the length of the side of the equilateral triangle.

Tip 4: How to find the median length

The median is the segment that connects the vertex of the triangle and the middle of the opposite side. Knowing the lengths of all three sides of the triangle, you can find it Medians. In particular cases of isosceles andAn equilateral triangle, obviously, it is enough to know, respectively, two (not equal to each other) and one side of the triangle. The median can also be found from other sources.

You will need

The lengths of the sides of the triangle, the angles between the sides of the triangle

Instructions

Consider the most general case of the triangle ABC with three sides that are not equal to each other. Length Medians AE of this triangle can be calculated by the formula: AE = sqrt (2 * (AB ^ 2) + 2 * (AC ^ 2) - (BC ^ 2)) / 2. Rest Medians Are completely analogous. This formula is derived via Stewart's theorem, or through the completion of a triangle to a parallelogram.

If the triangle ABC is isosceles and AB = AC,Then the median AE will be both the height of this triangle. Consequently, the triangle BEA will be rectangular. By the Pythagorean theorem, AE = sqrt ((AB ^ 2) - (BC ^ 2) / 4). From the general formula of length Medians triangle, for medians BO and CP is valid: BO = CP = sqrt (2 * (BC ^ 2) + (AB ^ 2)) / 2.

If the triangle ABC is equilateral, then obviously all of it Medians are equal to each other. Since the angle at the vertex of an equilateral triangle is 60 degrees, then AE = BO = CP = a * sqrt (3) / 2, where a = AB = AC = BC is the length of the side of an equilateral triangle.

The median of the triangle can also be found from otherData. For example, if the lengths of two sides are given, one of which is median, for example, the lengths of the sides AB and BC, as well as the angle x between them. Then the length Medians can be found in terms of the cosine theorem: AE = sqrt ((AB ^ 2 + (BC ^ 2) / 4) -AB * BC * cos (x)).

Tip 5: How to find the median length in a triangle

The median of the triangle is the segment drawn byFrom any of its vertices to the opposite side, while dividing it into parts of equal length. The maximum number of medians in the triangle is three, according to the number of vertices and sides.

Instructions

Problem 1. In an arbitrary triangle ABD, the median BE is carried out. Find its length if it is known that the sides are, respectively, AB = 10 cm, BD = 5 cm and AD = 8 cm.

Decision.Apply the median formula with the expression across all sides of the triangle. This is a simple problem, since all the lengths of the sides are known: BE = √ ((2 * AB ^ 2 + 2 * BD ^ 2 - AD ^ 2) / 4) = √ ((200 + 50 - 64) / 4) = √ ( 46.5) ≈ 6.8 (cm).

Task 2.In the isosceles triangle ABD, the sides AD and BD are equal. The median is drawn from the vertex D to the side BA, while making an angle with BA equal to 90 °. Find the median DH length, if it is known that BA = 10 cm, and the angle DBA is 60 °.

Decision.To find the median, determine one and the same sides of the triangle AD or BD. To do this, consider one of the rectangular triangles, say BDH. From the definition of the median it follows that BH = BA / 2 = 10/2 = 5. Find the side of BD by trigonometric formula from the property of a right triangle - BD = BH / sin (DBH) = 5 / sin60 ° = 5 / (√3 / 2 ) ≈ 5.8.

Now there are two possible options for finding the median: by the formula used in the first problem or by the Pythagorean theorem for a right-angled triangle BDH: DH ^ 2 = BD ^ 2 - BH ^ 2.DH ^ 2 = (5,8) ^ 2 - 25 ≈ 8,6 (cm).

Problem 3. In an arbitrary triangle BDA three medians are carried out. Find their lengths if it is known that the height DK is 4 cm and divides the base into segments of length BK = 3 and KA = 6.

Decision.The lengths of all sides are required to find the medians. The length BA can be found from the condition: BA = BH + HA = 3 + 6 = 9. Consider the right triangle BDK. By the Pythagorean theorem, find the length of the hypotenuse BD: BD ^ 2 = BK ^ 2 + DK ^ 2; BD = √ (9 + 16) = √25 = 5.

Similarly, find the hypotenuse of the right triangle KDA: AD ^ 2 = DK ^ 2 + KA ^ 2; AD = √ (16 + 36) = √52 ≈ 7.2.

From the expression formula through the sides, findMedians: BE ^ 2 = (2 * BD ^ 2 + 2 * BA ^ 2 - AD ^ 2) / 4 = (50 + 162 - 51.8) / 4 ≈ 40, hence BE ≈ 6.3 (cm). DH ^ 2 = (2 * BD ^ 2 + 2 * AD ^ 2 - BA ^ 2) / 4 = (50 + 103.7 - 81) / 4 ≈ 18.2, hence DH ≈ 4.3 (cm). AF ^ 2 = (2 * AD ^ 2 + 2 * BA ^ 2 - BD ^ 2) / 4 = (103.7 + 162 - 25) / 4 ≈ 60, hence AF ≈ 7.8 (cm).