LovesTheTeam.com

Instructions

1

To answer the question, is the randomthe value of the normal one, we can draw the concept of entropy H (x), which arises in information theory. The matter is that any discrete message formed from n symbols X = {x₁, x₂, ... xn}, can be understood as a discrete random variable given by a series of probabilities. If the probability of using a symbol, for example, x₅ is equal to P₅, then the probability of the event X = x та is the same. From the terms of information theory, let us take the concept of the amount of information (more precisely, our own information) I (xi) = ℓog (1 / P (xi)) = - ℓogP (xi). For brevity, write P (xi) = Pi. The logarithms here are taken on the basis of 2. In specific expressions, such grounds are not recorded. Hence, by the way, a binary digit (binary digit) is a bit.

2

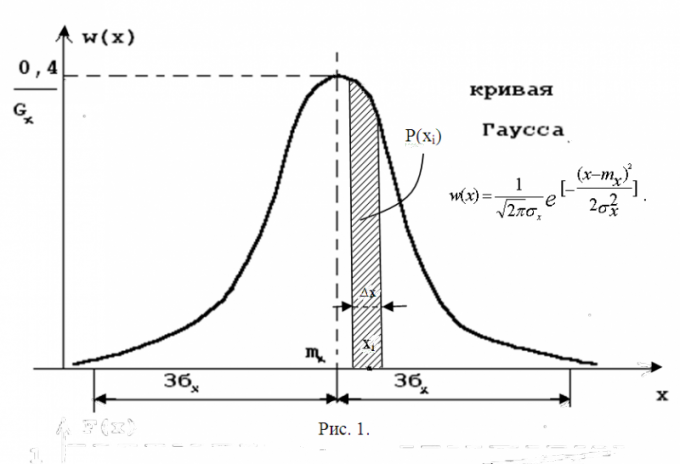
Entropy is the average number ofinformation in one value of the random variable H (x) = M [-ℓogPi] = - ΣPi ∙ ℓogPi (the summation is over i from 1 to n). And it has continuous distributions. To calculate the entropy of a continuous random variable, imagine it in a discrete form. Divide the portion of the range of values ​​into small intervals Δx (quantization step). As a possible value, take the middle of the corresponding Δx, and instead of its probability use the area element Pi≈w (xi) Δx. The situation is illustrated in Fig. 1. It shows, down to small details, a Gaussian curve, which is a graphical representation of the probability density of a normal distribution. Here the formula is given for the probability density of this distribution. Carefully consider this curve, compare it with the data that you have. Maybe the answer to the question has already cleared up? If not, it's worth continuing.

3

Use the methodology proposed in the previousstep. Make a number of probabilities of a now discrete random variable. Find its entropy and pass to the continuous distribution as n → ∞ (Δx → 0). All calculations are shown in Fig. 2.

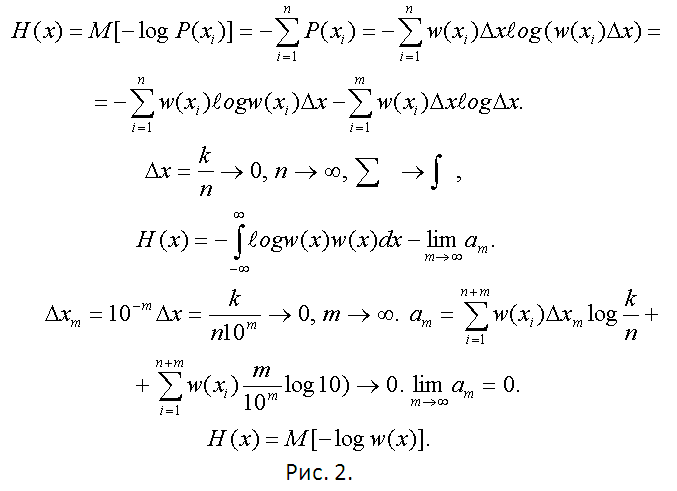
4

One can prove that normal (Gaussian)distributions possess maximum entropy in comparison with all others. By simple calculation, using the final formula of the previous step, H (x) = M [-ℓogw (x)], find this entropy. No integration is required. The properties of the mathematical expectation are sufficient. Obtain the H (x) = ℓog₂ (σх√ (2πe)) = ℓog₂ (σх) + ℓog₂ (√ (2πe)) ≈ℓog₂ (σx) +2,045. This is the maximum possible. Now using any data about the distribution available to you (starting from a simple statistical population), find its variance Dx = (σx) ². Substitute the calculated σx into the expression for the maximum entropy. Calculate the entropy of the random variable H (x) you are investigating.

5

Make up the ratio H (x) / Hmax (x) = ε. Independently select the probability ε₀, which can be considered almost equal to unity when deciding on the proximity of your distribution and normal. Call it, say, likelihood probability. Values ​​greater than 0.95 are recommended. If it turned out that ε> ε₀, then you (with probability at least ε₀) deal with the Gaussian distribution.