Tip 1: How to prove that a triangle is a rectangular
Tip 1: How to prove that a triangle is a rectangular
Among the many different shapes on the plane are polygons. The word "polygon" itself indicates that there are other angles in this figure. Triangle is a geometric figure bounded by three mutually intersecting lines that form three internal angles.

Instructions
1
There are different triangles, for example: an angle of less than 90 degrees, a rectangular triangle (one corner of such a triangle is exactly 90 degrees). Consider a rectangular triangle and its properties, which are established with the help of the theorem on the sum of the angles of a triangle. Theorem: the sum of two acute angles of a right triangle is 90 degrees. The sum of all angles in the triangle is 180 degrees, and the right angle is always 90 degrees. Therefore, the sum of the two sharp angles of a right-angled triangle is 90 degrees.

2
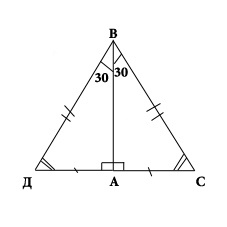
The second theorem: the cathete of a right triangle lying opposite the angle of 30 degrees is equal to half the hypotenuse. Consider the triangle ABC. The angle A will be straight, the angle B is 30 degrees, hence the angle C is 60 degrees. It is necessary to prove that AC is equal to one second BC. It is necessary to apply the triangle ABD to the triangle ABC. A triangle of BHD is obtained, in which the angle B is equal to the angle D, hence it is equal to 60 degrees, so the DS is BC. But AC is equal to one second DS. From this it follows that AC is equal to one second BC.

3
If the cathete of a right triangle is equal tohalf of the hypotenuse, then the angle lying against this leg is 30 degrees - this is the third theorem. It is necessary to consider the triangle ABC, in which the AU loop is equal to half the sun (hypotenuse). Let us prove that the angle of ABC is 30 degrees. Attach the triangle ABD to the triangle ABC. Should be an equilateral triangle of VSD (ВС = СД = ДВ). The angles of such a triangle will be equal to each other, so each angle is 60 degrees. In particular, the angle of the internal combustion engine is 60 degrees, and the angle of the internal combustion engine is equal to two angles of the ABC. Consequently, the angle of the ABC is 30 degrees. Q.E.D.
Tip 2: How to prove that triangles are equal
Two triangles are equal if all elements of the sameare equal to the elements of the other. But it is not necessary to know all the dimensions of the triangles in order to conclude that they are equal. It is enough to have certain sets of parameters of given figures.

Instructions
1
If it is known that two sides of the sametriangles are equal to the two sides of the other and the angles between these sides are equal, then the triangles under consideration are equal. For the proof, combine the vertices of equal angles of two figures. Continue the overlay. From the point common to two triangles, point one side of the angle of the superimposed triangle along the corresponding side of the bottom figure. By convention, these sides in two triangles are equal. Hence, the ends of the segments coincide. Consequently, another pair of vertices in the given triangles was combined. The directions of the second sides of the angle from which the proof is initiated will coincide because of the equality of these angles. And since these sides are equal, the last vertex will overlap. Between two points it is possible to hold a single straight line. Consequently, the third parties in the two triangles coincide. You have obtained two completely matched figures and a proven first sign of equality of triangles.
2
If the side and the adjacent two corners in onetriangle are equal to the corresponding elements in another triangle, then these two triangles are equal. To prove the correctness of this statement, put two figures, combining the vertices of equal angles with equal sides. Because of the equality of the angles, the direction of the second and third sides will coincide and the place of their intersection will be uniquely determined, that is, the third vertex of the first of the triangles necessarily coincides with the analogous point of the second. The second criterion for the equality of triangles is proved.
3
If three sides of one trianglerespectively, are equal to three sides of the second, then these triangles are equal. Align the two vertices and the side between them so that one figure is over the other. Place the circular needle in one of the common vertices, measure the second side of the lower triangle and draw this radius on the upper half of the composition of two triangles. Now repeat the operation from the second aligned vertex with a radius equal to the third side. Make a notch at the intersection with the first arc. The intersection point of these curves is only one, and it coincides with the third vertex of the upper triangle. You have proved the statement, which in geometry is called the third sign of equality of triangles.







